爱哲数学老师获奖论文 | 聚焦数学建模过程：《自行车中的数学》教学设计

写在前面

在由北京数学会中学委员会主办的“第11届中小学数学教师论坛”上，爱哲数学老师赵博士的“聚焦数学建模过程：《自行车中的数学》教学设计”获得了数学教育教学研究成果奖（教学设计）。

人教六年级下综合与实践活动“自行车中的数学”是一个数学建模问题，旨在让学生经历提出问题——分析问题——建立数学模型并求解——解决问题的过程，体验用数学解决实际问题的思考方法，提升模型意识和应用意识。

在课例中，赵博士对探究的核心问题进行了再设计，引导学生探究真实情境中自行车的速度。学生利用资料深入理解自行车的传动原理，从而选择数学建模的关键变量，描述变量之间的数量关系，最终建立数学模型，求解自行车的速度。学生在探究这一真实问题的过程中，可以体验更加复杂完整的数学建模过程，得到的结论与现实生活联系也更加密切。

本教学设计涉及简单机械、能量转换的知识，可能进一步延伸成为跨学科主题学习的一部分。

 

1

教学背景分析

01

教学内容与分析

“自行车中的数学”是人教版义务教育数学教材六年级下册中的一个综合与实践活动。本课内容位于“比例”单元的末尾，旨在让学生运用所学的圆、排列组合、比例等知识解决实际问题。通过解决生活中常见的自行车里的问题，了解数学与生活的广泛联系，经历“提出问题——分析问题——建立数学模型——求解——解释与应用”的问题解决的基本过程，获得运用数学解决实际问题的思考方法，并加深对所学知识及其相互关系的理解（《义务教育教科书教师教学用书六年级下册》）。

本课由两个探究性活动组成，探究的问题分别是：

自行车蹬一圈能走多远；

变速自行车能变化出多少速度。

在前一个问题中，学生基于自行车传动结构的原理，探究前后齿轮齿轮齿数和转数之间的反比例关系，结合车轮直径的数据，建立数学模型（等式），计算自行车蹬一圈车轮前进的距离。

在后一个问题中，学生可以应用之前建立的数学模型，探究变速自行车能变化出多少速度，并比较在不同齿比下自行车蹬一圈前进的距离。

 

01

同题材常见教学思路综述

作为探究性活动，本课的结构一般包含以下环节：

创设情境、提出问题：教师直接提出探究问题“自行车蹬一圈能走多远”。

课堂交流、方案比较：学生一般会提出直接测量的方案，教师通过一定的引导，指出直接测量的不足，引导学生使用数学建模的方法来解决问题。

观察自行车结构、分析问题

教师引导学生通过观察自行车的结构，得到“前齿轮转一个齿，后齿轮也转一个齿”这一关键的等量关系；随后在前齿轮转数和脚蹬圈数之间建立联系，在后齿轮转数和车轮转数之间建立联系。

建立数学模型并求解：对上面的关键等量关系进一步细化，最后得到以下关系式：

应用并检验模型：提出第二个问题“变速自行车能变化出多少速度”及衍生问题“何时蹬一圈前进最远”，学生应用之前的模型解决问题并汇报结果。

课堂练习：学生解决“已知车轮直径、前齿轮齿数、后齿轮齿数，求蹬一圈前进多远”类型的应用题。

课堂小结。

 

01

我的思考（含学生分析）

本课实际上是一个典型的数学建模问题，学生需要建立数学模型去解决一个现实生活中的问题。根据《数学义务教育课程标准（2022）》，数学建模的基本过程包括：从现实生活或具体情境抽象出数学问题；用数学符号表示数学问题中的数量关系和变化规律；求出结果并讨论结果的意义。在本课时中，数学问题是“自行车蹬一圈能走多远”。

教师引导学生探究这一问题中蕴含的数量关系，得到结论：

 

最后，运用结论解决一些相关的问题。

 

 

从数学建模的视角来看，本课常见教学设计存在以下一些问题：

 

首先，“自行车蹬一圈能走多远”问题本身稍显生硬，不够自然。人们在讨论自行车的性能时，往往会问：这车能骑多快？而很少会问：这车蹬一圈能走多远？自行车的速度是一个有用且常用的指标，但 “蹬一圈能走多远”这个指标很不常用，作为探究的问题，显得过于琐碎、牵强，不容易引起学生的兴趣。

 

其次，低估了建模的过程复杂性，或者为了补偿这点而人为简化了建模的过程。为解决实际问题而建立数学模型的时候，一个关键问题是：哪些量与这个问题相关？或者说，应该选择哪些变量来建立数学模型？解决真实问题时，选择变量可能比描述变量之间的关系更困难。

 

在本问题中也是如此：如果能发现影响自行车“蹬一圈能走多远”的关键因素（变量）是前后齿轮的齿数和车轮直径/周长，解决问题就变得比较容易了。

 

然而要发现这一点，需要学生对自行车的机械原理和机械结构有清晰的认知；而实际上，学生对此认识较为模糊，因此解决问题有困难。为了补偿这一点，教师和教材会直接引导学生去关注自行车的齿轮和齿数（如下图），相当于给出相关的变量，学生只需要研究这些变量之间的数量关系。这么做降低了探究的难度，但是降低复杂性也就意味着破坏了数学建模过程的真实性和完整性。如果本课的目的是要感知数学建模的基本过程，那么保留过程的复杂性和真实性似乎更为必要。

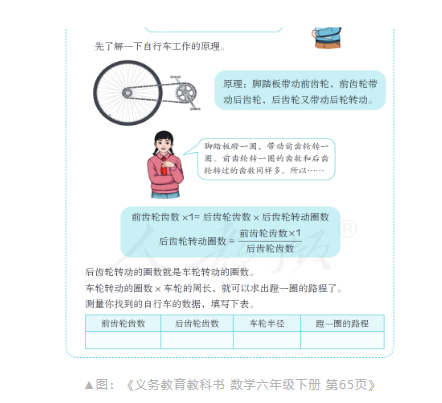
根据以上问题和以往教学实践中学生的情况，我的教学设计与常规教学思路相比，有以下主要改动：

 

第一， 将本课的探究问题由“蹬一圈自行车能骑多远”，改为“Z老师（本人）骑自行车能骑多快”。作者本人恰好常骑自行车，学生也常看到我骑车来校，因此这个问题对他们更切身相关、也更自然。

 

第二， 用更多的时间引导学生认识自行车的机械结构，从而深入分析问题。为此，使用系列图片，简要引导学生回顾自行车的结构发展的历史。这样做的目的是引导学生把视线聚焦到现代自行车的齿轮/链条传动结构上，注意到齿轮/链条传动结构的目的就是为了使“脚蹬一圈，车轮前进多于一圈”，从而更加主动地去探究 “自行车蹬一圈能走多远”的问题，在这个过程中自主地选择与解决问题相关的变量（轮径、前齿轮齿数、后齿轮齿数），完成建模的最关键步骤。

 

第三， 可以看到，比起“自行车蹬一圈能走多远”，要解决“自行车能骑多快”的问题需要增加一个已知量，那就是蹬车的频率。获得这个数据有三种可能的方法：实际测量；查阅文献；教师直接给出假设。无论是哪一种方法都是数学建模中获得数据的常用方法。在这一过程中，学生可以进一步感知数学建模的基本过程。

 

2
教学目标与重难点

 

01

教学目标

 

体验数学建模的基本过程，经历“提出问题——分析问题——建立模型——求解——解释与应用”的过程，培养模型意识。

 

使学生综合运用所学知识解决实际问题，体验数学与生活的联系，培养应用意识。 

 

02
教学重点

 

将实际问题转化为数学问题，选择合适的变量，描述变量之间的数量关系。

 

03

教学难点

 

选择对于解决问题关键的变量。

 

3
教学过程

 

01

教学过程流程图（或问题框架）

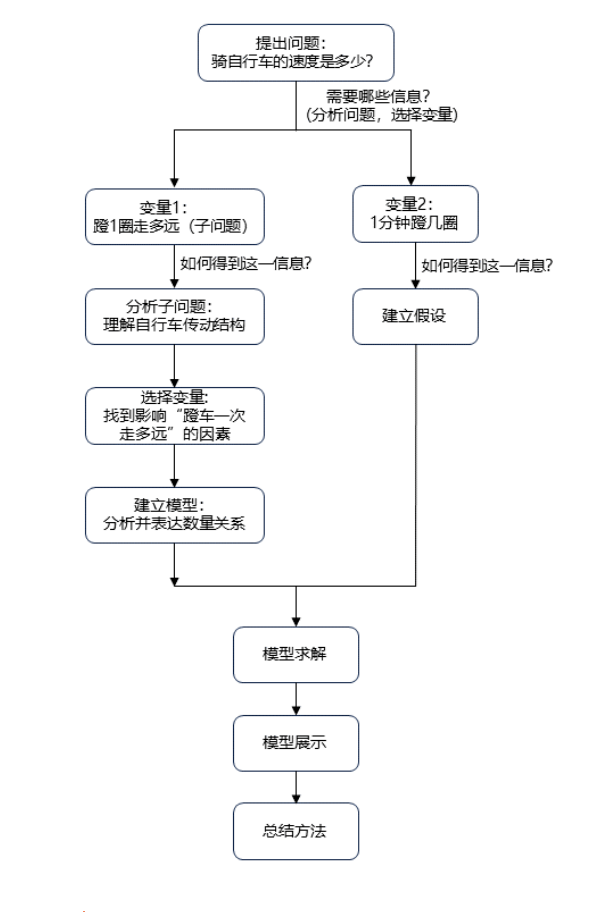
02

教学活动

 

教学环节包括分析问题&选择变量、分析子问题、选择变量、建立模型、建立假设、模型求解、模型展示、课堂小结等环节。此部分略去，如需详细教学活动流程，请在公众号后台留言咨询。

 

03

板书设计

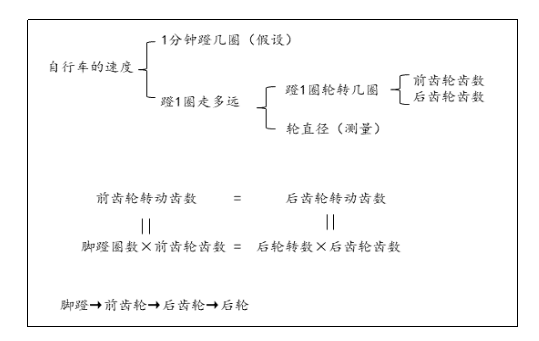
4

教学反思（或进一步思考的问题）

根据教学的情况，本教学设计可能在以下两处可以再做优化：

合作探究：教学过程中，建立模型这一部分总体较为线性，由教师引导学生一步步得出结论。因为前期支撑已经较多，本部分可以考虑放手让学生以小组探究的形式得出结论，更能激发学生的主动性，教学环节也可以相对简洁。

评估：本组课时的评估可以让学生以书面的形式（例如制作手抄报）再次梳理解决问题的过程、结论和方法，归纳知识之间的联系，总结探究的方法，深化对数学建模基本过程的理解，交流各自的收获。

此外，我们认为这一教学设计具有进一步拓展，作为跨学科主题学习的一部分的潜力。

首先，课堂学习的过程已经涉及对简单机械的理解。

其次，当我们讨论可以变化齿比从而改变自行车的速度时，可以自然地带来这些问题：我们应该怎样选择变速自行车的齿比？高齿比和低齿比分别有什么优势和劣势，分别适应什么情况？改变齿比，自行车的速度可以无限提升吗？为什么不能？

这些问题涉及到力、做功、能量之间的关系和转化，是科学研究的范畴，同时与本课的关系自然且紧密。跨学科的教学设计可以成为下一步思考的问题。